お知らせ
第五章 国際標準化~筆者の歩んだ道(そのII)
5.1 琉大から東北大の虫明研究室へ卒業論文留学
1972年に、沖縄が本土に復帰した記念として、日本電信電話公社(NTT)が「無線通信のマイクロ波による見透し外通信による電話回線」で、鹿児島から沖縄まで約500km、島伝いに電話工事を行っていた。筆者は、琉大理工学部電気工学科3年次だったが、琉大祭で「対流圏散乱によるマイクロ波の見透し外無線通信」に関する調査・研究の成果を発表した。筆者は幸いにも、沖縄が本土復帰した直後で1972年電気工学科4年次の後学期の9月から、パスポートを持って東北大工学部通信工学科の虫明研究室(虫明研)へ卒業論文(卒論)留学する機会に恵まれた。
虫明康人先生に「無線通信」の「マイクロ波やミリ波の電波伝搬の研究をしたい」と申し上げたところ、先生は『沖縄の琉大ではすぐ研究できないかもしれないが、これからは光の時代だから「光通信」の研究をしなさい』と言われた。ご存じのように、虫明康人先生は「自己補対アンテナと虫明の関係式」で、「無線通信」のアンテナと電波伝搬の分野でIEEE(米国電気学会)マイルストーンに認定された世界的な大家であるにも関わらず筆者にこれからの将来を見越して「光通信」の研究を勧めて下さったので虫明先生の「先見の明」に大変感謝している。
筆者は、東北大の虫明康人教授と工藤正昭助手(工学博士、元仙台高等専門学校)のご指導のもとで、1973年の4年次に工学士の学位の卒論を行い、研究テーマは、「光無線通信」の「光伝送におけるビーム間の空間的な漏話について」のレーザビームの空間伝搬に関する研究であった。筆者は、東北大の虫明研でも卒論発表をして、沖縄の琉大の理工学部電気工学科でも卒論発表を行った。東北大へパスポートを持って卒論留学した時は、琉球政府立琉大だったが、沖縄へ一時的に帰省した時は、国立琉大に変わっていたため、国立琉大理工学部電気工学科の第1期生になるような激動の時期だった。
虫明研で卒論を始める前に、大学院修士課程の大学院入試を受験したが、実力不足で不合格となった。その時、成績が悪かったので、虫明先生から「大学院に行くことだけが人生のすべてではないので、ほかの仕事を探しなさい」と言われたのを今でもはっきり覚えている。これまで、琉大の電気工学科卒の優秀な先輩たちは、「国立4帝国大学の大学院には2年浪人しないと入れない」というジンクスがあった。しかし、筆者は、1年浪人でだめなら虫明先生のアドバイスのように別の仕事(教員など)をしようと強い決意をし、宮本武蔵のように真剣勝負で1年間必死で東北大大学院の過去問題などを中心に独学で集中して勉強したおかげで、翌年東北大の大学院入試に1年浪人で合格することができた。その時、虫明先生が笑顔で「今回は良い成績だったので安心している」と言われほっとしたのを今でも覚えている。
筆者がこれまでの「琉大電気工学科から2年浪人しないと帝国大学の大学院に合格できない」というジンクスを初めて破ったため、その後、1年浪人で合格する後輩たちが出てくるようになり、その数年後から現役でも合格する後輩たちも出てきたので、筆者は後輩たちに希望の扉を開くことができたのではないかと自負している。
5.2 オリジナリィティのある研究テーマの探し方
筆者が卒論をしていた頃、筆者の卒論を指導して下さった工藤正昭先生(図13)と同じ虫明研で博士課程の同級生だった土屋治彦氏{工学博士、当時NTT武蔵野電気通信研究所基礎研究部第三研究室(基礎3研)、元宇都宮大学教授、現山梨大学客員教授}が、NTT基礎3研の部下の光ファイバの融着接続に関する工学博士学位論文審査のため同行して虫明康人教授を訪れていた。筆者は、工藤先生と卒論では、He-Neガスレーザ光線をレンズによる空間伝送する光無線通信の研究をしていた。
その時、筆者の先輩の修士2年次の松本敏和氏(元NEC)は、工藤先生のご指導のもとで、修士論文の研究テーマのレンズによるレーザ光線の空間伝送の実験をしていた時に、レンズを固定していたねじを強く締めた時(非軸対称外部応力)に、レーザ光線の偏波(光)が回転する現象があることを偶然発見していた。
ガラスのような弾性体に外力(応力:Stress)を加えると、弾性体内部に応力分布が生じ、それによってひずみ(Strain)が生じる。このひずみによって弾性体内部に新たな光学異方性(複屈折:Birefringence)が現れる。この現象は”光弾性効果(Photo-Elastic Effect)”として建築工学や土木工学の分野ではよく知られている現象だったが、筆者は、この”光弾性効果”による偏波(光)が回転する現象を光ファイバに応用した研究を修士論文のテーマにしたいと決意した。幸いにも丁度その頃、NTT基礎3研から虫明研へ奨学寄附金を出して頂いていたこともあり、その当時では大変貴重な光ファイバを 提供して頂いたのでその光ファイバを用いて筆者の修士および博士学位論文作成に大いに役立てることができたので大変感謝した。
その頃は、光の「有線通信」の光ファイバ通信の夜明け前のあけぼの時代で、NTT電気通信研究所で光ファイバを製造していたので筆者にとっては大変ラッキー(幸運)だった。従って、筆者は光の「有線通信」の光ファイバ通信のあけぼの時代に若い大学院の修士時代から関わることができたことは大変恵まれており、現在でも虫明研の先輩の土屋治彦氏には 、色々ご指導して頂いており大変感謝している。
大学院生(院生)の研究の指導方法には、大きく分けて2つあるものと思われる。一つは指導教員の先生が院生に研究テーマを与えるタイプと二つ目は、院生本人に研究テーマを探させるやり方である。研究テーマを与える前者の方法は、指導者の先生がある程度研究結果を予測できるため、論文も比較的数多く発表できるが、短所としては、大学院修了後指導者の先生から離れた環境に置かれた時(就職後)に、オリジナリィティ(独創性)のある研究テーマを自分一人で探せないでいる研究者をこれまで数多く見てきた。
一方、虫明先生の指導方法は、後者の方法で「研究は、研究テーマを自分で探すところからスタートする」という厳しい指導方針なので大変苦労したが、最終的にはオリジナリィティのある研究テーマを自ら探せることができ、最初の頃の論文作成数は少なかったが、結果的にはオリジナリィティがあり、かつ質の高い論文を数多く発表できることを体験できたので、虫明先生の研究指導方法が優れているのではないかと確信でき感謝している。これは、その後のKDD研究所や琉大でオリジナリィティのある研究テーマの探し方や論文作成する際に大いに役に立った。しかし、これまで琉球大学で4年次の卒論を指導してきた経験より、学生は研究の仕方がよく分からないので研究指導者が研究テーマを与える方法がいいのではないかと考えている。
以上のように、虫明研では、大学院生の研究テーマは自分で探さなければならなかったので、建築工学科や土木工学科へ自分一人で行き、応力と光弾性効果の研究分野について自ら情報を収集し、これを光ファイバの応力と偏波(光)特性の研究に応用することができた。
結果的には、筆者の“光弾性効果”に着目した光ファイバの偏波(光)特性に関する研究は、先駆的な研究であるとして国際的に評価されたので虫明先生の研究テーマの探し方の指導方法が優れていることを実証することができ今でも心から感謝している。
筆者は、修士学位論文(1976年)では「光ファイバにおける(屈折率が“光弾性効果”によりx、y、z軸方向で異なる)異方性に関する研究」を、また、博士学位論文(1979年)では「光ファイバの伝送特性に及ぼす応力効果に関する研究」を行い、工学博士の学位取得後1979年4月に国際電信電話(株){KDD(KDDI)}研究所に入社した。KDD研究所での研究成果については後述する。
5.3 光ファイバの偏波(光)特性に及ぼす一方向の非軸対称外力の影響
筆者の東北大大学院における修士学位論文をまとめ1977年に“光ファイバの伝送特性に及ぼす機械的圧力の影響”として、(一社)電子通信学会の論文誌に投稿した結果、学術論文[12](図25)として採択された。その論文は、筆者の最初の日本語の論文で、その後は英語の論文が多くなったが、米軍の研究所から英文への翻訳の依頼が虫明康人教授にあり、虫明教授、工藤正昭助手と筆者の3人で英訳した筆者の論文を、米軍の研究所へ送付した結果、非常に高く評価され、光ファイバセンサー用として実用化されたようである。
修士及び博士学位論文審査の筆者の副査であった“W型光ファイバやフォトニック結晶技術の研究”等で世界的に著名な川上彰二郎教授(工学博士、東北大名誉教授)が光ファイバの偏波(光)特性関連では世界的に著名なProf. Dr. R. Ulrich(ドイツのハンブルグ大学名誉教授)に、この英訳した筆者の論文[12]を紹介して下さったことは、その後の筆者の研究業績の中で最も大きなウエートを占めることとなった。何故なら、Prof. Dr. R. Ulrichや彼の門下生達が彼らの論文に、よく筆者の(一社)電子通信学会の上記の論文[12]を数多く引用して下さり、筆者の光ファイバの偏波(光)特性に及ぼす応力の光弾性効果に関する論文を世界的にアピールしてくれたことによるところが大きかった。
以前、欧州(EU)最大の光通信関連の国際会議(ECOC:European Conference on Optical Communication)で、初めてProf. Dr. R. Ulrichに国際会議の会場でお会いした時遠くから“1977”と英語で言いながら筆者と笑顔で握手して頂いたことを時々懐かしく思い出すことがある。
それは、筆者が1977年に発表した最初の論文である“光ファイバに一方向から外力(非軸対称外部応力)が加わった場合の偏波(光)特性”に関する(一社)電子通信学会の論文[12]を高く評価して下さったことを体現して下さったからである。
光は、“粒”であるという“粒子説”と“波”であるという“波動説”の両方の性質を有しているが、ここでは、“波動説”の観点から述べることとする。光波は、電磁波(電波)の一部で、波長(色)が 0.38 [μm(ミクロン)]から 0.76 [μm]の虹の7色を可視光と呼んでいる。
ここで、1 [μm(ミクロン)] = 1/1000 [mm(ミリ)]の関係がある。
光波を含む電磁波は、電界Eと磁界Hが互いに直交(90°方向が異なる)しながら、進行方向に対し垂直に振動する横波であるが、太鼓の音は縦波である。光には、平均的にいずれの方向に対しても同じ強さで振動しながら進行する“自然光”と、透明な物質に一定の角度で入射した場合に見られる反射光が一つの面でしか振動しなくなる “偏光”がある。“偏光”は、電界ベクトルEの大きさと方向で表される。
電界ベクトル E は、x軸成分(Ex)と y軸成分(Ey)に分けられるが、Ex とEy の位相差がゼロの場合は、直線的に振動しているので直線偏波(光)という。この直線偏波(光)成分のみを通過させる(フイルタリングする)光デバイスを偏光子(ポラライザ)というが、同じ光デバイスでも受光器の前に置いて、偏波(光)成分を分析する場合は、検光子(アナライザ)という。
分かりやすい例を挙げると、偏光子は、偏光板(偏光フイルタ)とも呼ばれており、自動車の窓ガラスに偏光フイルタとして“カーサンバイザー”を張り付けると道路からの乱反射のまぶしい光を抑えることができ、“偏光サングラス”や“カメラ用偏光フイルタ”なども商品化されている。
電界ベクトル E の x軸成分(Ex)と y軸成分(Ey)の位相差が90°で、Ex と Ey の強度が異なる場合の電界ベクトル E の軌跡は楕円軌道になるがこれを楕円偏波(光)といい、Ex と Ey の強度が同じ場合は、円偏波(光)という。
図25は、裸光ファイバに一方向の非軸対称の外力を加えた場合、荷重方向に対して0°と90°以外の方向に直線偏波(光)Ei を入射した場合に直交偏波(光)成分が発生するのを検証する実験システムとその実験結果を示している[12]。
①光ファイバに一方向から外力を加える非軸対称外力荷重装置を示している[12]。光ファイバは、折れやすいので機械的強度を付与するため、2層の樹脂で被覆(コーティング)されている。コーティング材には、紫外線硬化樹脂(UV)等が使用されていた。その被覆の除去は、非常に危険ではあったが濃硫酸(H2SO4)を用いて化学的に被覆除去処理を行った。裸光ファイバ長を L [cm]とすれば、荷重W [g]は、f [g/cm]・L [cm] となる。
②裸光ファイバに一方向から単位長当たりの荷重 f = W/L [g/cm] を加えた場合の光ファイバの直交偏波(光)
成分発生実験システムを示している。光源は、波長 λ=0.6328 [μm]で直線偏波(光)の赤色の He-Neガスレーザを用いた。使用した光ファイバは、ステップインデックス形屈折率分布のシングルモード光ファイバで、その構造パラメータは、コア径 2a ≒ 6 [μm]、クラッド径 2b ≒ 125 [μm]であった。
コアとクラッドの非屈折率差 Δ≒ {(n1-n2)/n1} x100 [%] = 0.24 [%] のシングルモード光ファイバを用いた。ここで、n1 は、光ファイバに光波が通る中心部のコアの屈折率で、n2は、コアを取り囲むクラッドの屈折率を表す。一般的に、n2 は、石英(SiO2)ガラスの屈折率を表す。
通常光ファイバのコアには、石英(SiO2)ガラスにGe(ゲルマニウム)などの不純物を添加(ドープ)して、クラッドの屈折率より少し高めにするようにして光波が伝送できて、光通信ができるように設計されている。
物質中の光速度 v は、真空中の光速度 c より遅いことが知られているが、物質中の光速度 v と真空中の光速度 c の比 n=c/v を屈折率という。
以下に、代表的な物質の屈折率を示す。
真空:1.0, 空気:1.000293, 水:1.333, 石英ガラス:1.458, 窓ガラス:1.500, ダイヤモンド:2.419
少し脱線するが、ダイヤモンドは、天然の物質としては最高の屈折率を有しており、カットをうまくやると光を波長(色)別に分散させ7色の光に燦然と輝かせることができるので、高価な宝石となっている。
③光ファイバの出力端における偏波(光)面の座標系を示す。ここで、外力 f [g/cm]を荷重する方向を x 軸とし、入射偏波(光)角 θi に対する座標系をX-Y軸とするが、0°と90°以外の 0°<θi<90° で、特に θi=45° の場合、外力を加えた場合に発生する楕円偏波(光)面の新しい座標系は、ξ−η 軸になる。ここで、x,y,z 軸の座標系は、工学分野で用いられている x軸 から y軸 方向に回転した場合、右ねじの進む方向を z軸 の正方向とする座標系を用いているが、一般的には、理数系分野で用いられているx軸からy軸を回転した時に左ねじの進む方向をz軸の正とする座標系を使用する場合もある。
④光ファイバに、X軸方向に偏波(光)した直線偏波(光)Ei を入射し、x 軸 方向から外力を加えた場合、光ファイバの出射端の偏光板を、外力を加えない時の入射偏波(光)面の座標系 x-y 軸 に合わせて、光ファイバに外力を加えていった場合、内部に発生する楕円偏波(光)の長軸の ξ 軸と短軸の η 軸成分の受信光パワーを測定した。外力に対する入射偏波(光)成分(Ei)と直交偏波(光)成分の長軸の ξ 軸(Eξ)と短軸の η 軸成分(Eη)の受信光パワーの測定結果を示している。
入射偏波(光)角 θi が、0°と90°の場合には、入射偏波(光)成分 Ei と直交偏波(光)成分の受信光パワーのカーブは交差しないが、 θi が、45°の場合には、直交偏波(光)成分が発生するため交差することが分かった。その結果、0°と90°の場合には、偏波(光)面の主軸の変化はないが、 0°<θi<90° の場合で、特に θi=45° の場合には、屈折率が異方性になりクロストーク(漏話)が発生するので、入射した偏波(光) Ei は、直線偏波(光)⇒楕円偏波(光)⇒円偏波(光)⇒直線偏波(光)の順で偏波(光)面が回転していくことが分かる[12]。
後述するが、これが、偏波面保存ファイバ(PMF:Polarization Maintaining Fiber)の基本原理に関係する重要な発見であった[12]。
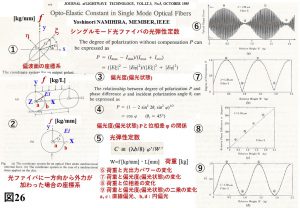
図26に、東北大での修士論文をまとめた文献[12]をKDD研究所で発展させて米国電気学会IEEEの権威あるJLT(Journal of Lightwave Technology)の英文誌に投稿し採択された筆者の“Opto-Elastic Constant in Sigle Mode Fibers(シングルモード光ファイバの光弾性定数)”[13]の論文の概要を示す。
東北大の虫明研では、光ファイバの光弾性定数までは、求めることはできなかった。しかし、光通信用に用いられる石英系シングルモード光ファイバの光弾性定数が分かれば、外部応力や内部応力と偏波(光)特性のメカニズムを明らかにすることが可能で、光ファイバセンサー等への応用が広がり重要な研究テーマになるため光ファイバの光弾性定数を求めることにチャレンジした。
東北大の虫明研では、研究予算が少なかったため、光源の使用波長として、波長 λ = 0.6328 [μm]で直線偏波(光)の赤色の He-Ne ガスレーザしか使用できなかったが、KDD研究所では、筆者が入社後約4年(1983)頃使用できた研究予算は、東北大の虫明研に比べ数100倍あったため、光源として、波長0.63 [μm]の He-Ne ガスレーザの他に, 0.85 [μm], 1.15 μm , 1.19 μm, 1.30 μm, 1.50 μm, 1.51 μm, 1.58 μm の複数の波長の光源を用いることができ、石英系シングルモード光ファイバの光弾性定数の波長特依存性の実験を行うことができたので大変恵まれており感謝している[13]。
図26より、以下に石英系シングルモード光ファイバの光弾性定数を導出するまでの過程を示す[13]。
①光ファイバの出力端における偏波(光)面の座標系を示す。ここでは文献[12]とは違って、裸光ファイバに一方向から非軸対称の外力を加える方向を y軸 としている。単位長当たりの外力 f [kg/mm] を加えた場合に発生する楕円偏波(光)面の座標系は、新たに ξ−η 軸とする。ここでは、理数系分野で用いられているx軸から y軸 を回転した時左ねじの進む方向を z軸 の正とする座標系を用いているので、後方から手前の進む方向が z軸 の正方向になる[13]。
②裸光ファイバに単位長当たりの非軸対称外力 f [kg/mm] を加えた場合の座標系で、文献[12]とは、x軸 と y軸 が反対になっているが特に問題はない。KDD研究所でも、光ファイバの被覆の除去は、非常に危険ではあったが、東北大の虫明研と同様に濃硫酸(H2SO4)を用いて化学的に被覆除去処理を行った。
③Pは、偏光補償の無い偏光度(DOP:Degree of Polarization)なので、偏光状態 SOP(State of Polarization)と同じである[13]。
P= 1.0 の時 直線偏波(光)で、P = 0 の時 円偏波(光)となるが、それ以外は、楕円偏波(光)になる。
P = (Imax – Imin )/(Imax + Imin )
{Imax: 楕円偏波(光)の長軸(Eξ)の光パワー、Imin:楕円偏波(光)の短軸(Eη)の光パワー}
④偏光補償の無い偏光度(偏光状態)Pと位相差ϕの関係式を示す[13]。
P=cosϕ {ϕは荷重f [kg/mm]の関数である}
⑤シングルモード光ファイバの光弾性定数 C を求める式である。C ≒ (λb/8)ϕ’/W’ ここで、λ は、使用波長であり、2b は、クラッド径であるので、(λb/8)は、既知の値で、光弾性定数 C が求められる。
⑥光通信の代表的なシステム波長λ=1.30 μmにおける、相対荷重W’に対する検光子(アナライザー:直線偏光成分を抜き出す素子)を通過した後の光出力パワーの変化を示す。ここで、ⓐ, ⓑ, ⓒ, ⓓ は、直線偏波(光)⇒円偏波(光)⇒直線偏波(光)⇒円偏波(光)を表している。ただし、(ⓐ–ⓑ)と(ⓒ–ⓓ)間は、楕円偏波(光)になる。
⑦光通信の代表的なシステム波長 λ=1.30 μmにおける、相対荷重 W’に対する偏光度(偏光状態)の変化を示す。ここで、ⓐ, ⓑ, ⓒ, ⓓ は、直線偏波(光)⇒ 円偏波(光)⇒ 直線偏波(光)⇒ 円偏波(光)を表している。ただし、(ⓐ–ⓑ)と(ⓒ–ⓓ)間は、楕円偏波(光)になる。
⑧光通信の代表的なシステム波長 λ=1.30 μmにおける、相対荷重 W’に対する相対位相差 ϕ’の変化を示す。ここで、ⓐ, ⓑ, ⓒ, ⓓ は、直線偏波(光)⇒ 円偏波(光)⇒ 直線偏波(光)⇒ 円偏波(光)を表している。ただし、(ⓐ–ⓑ)と(ⓒ–ⓓ)間は、楕円偏波(光)になる。実験結果より、相対位相差 ϕ’と相対荷重 W’は、ϕ’= (8C/λb)W’ で、リニア(線形性)の関係になることが分かった。
従って、その直線の傾き角が(8C/λb)となる。
ここで、λ は、使用波長であり、2b は、クラッド径であるので、(8/λb) は既知の値で、念願の光弾性定数 C が求められることが分かる。
光通信の代表的なシステム波長 λ=1.30 μm 及び λ=1.55 μm における光弾性定数は、C ≒ 3.2×10-5[mm2/kg] 及び C ≒ 3.0×10-5 [mm2/kg] が得られている[13]。
⑨光通信の代表的なシステム波長 λ=1.30 μmにおける、相対荷重W’に対する偏光度(偏光状態)の二乗の変化を示す。ここで、ⓐ, ⓑ, ⓒ, ⓓ は、直線偏波(光)⇒ 円偏波(光)⇒ 直線偏波(光)⇒ 円偏波(光)を表している。ただし、(ⓐ–ⓑ)と(ⓒ–ⓓ)間は、楕円偏波(光)になる。
5.4 偏波面保存ファイバの基本原理の発見
光ファイバ中で直線偏波(光)面を保存し、さらに外乱に対してもその偏波面の保存性を維持できる光ファイバは、光伝送及び光計測・センシングの分野で、重要な役割を果たす。このような光ファイバは、偏波面保存ファイバ(PMF:Polarization Maintaining Fiber)と呼ばれ、その断面内で複屈折性を有しているのが特徴である。作製法としては、光ファイバ断面内に非軸対称の応力を付与する方法、非軸対称の幾何学構造的屈折率分布を与える方法、及びこれら2つの効果を複合する方法がある。
図27の、筆者の一方向から(非軸対称)外力が加えられた光ファイバの偏波特性に関する論文[12]は、光ファイバ断面内に非軸対称の応力を付与する方法に寄与しており、光ファイバジャイロなどに使用されている偏波面保存ファイバ(PMF)の中でも良く商用化されている“PANDA:Polarization-maintaining AND Absorption-reducing(パンダ)ファイバ”の基本原理として国内外の専門家には知られている。そのエピソードの一例として、NTT研究所の佐々木豊博士(元茨城大学教授)が、「筆者の東北大の修士論文を内緒(残念ながら筆者の論文[12]は引用されていなかった)で取り寄せ筆者の論文[12]を参考にして“偏波面保存光ファイバ(PMF)”では有名な“PANDA(パンダ)ファイバ”(図27)[14]を発明した事につながった」と筆者の友人でもある佐々木豊先生が、ずいぶん後になってオーストラリアのシドニー市で開催された国際会議で一緒になった時に筆者に語ってくれたことがあった。
図27で、①は、裸光ファイバに単位長当たりの非軸対称荷重 f [g/cm] = W [g] /L [cm] を加えた場合の主応力成分と位相差や速波軸や遅波軸の関係を示している。筆者の文献[12]と[13]で、座標系が工学分野の右ねじの進む方向を z 軸の正方向とするか、理学分野の左ねじの進む方向を z 軸の正方向とするかの違いがあり、x 軸と y 軸の違いはあるが、座標系の変更だけなので特に問題はない。図27では、光ファイバの中心のコア部分には、x 軸方向に圧縮応力 σx が発生し、y 軸方向には、引張応力 σy が発生する[12]。
σx ≒ -3f / (πb) 、σy ≒ f / (πb) (π ≒ 3.14、2b:クラッド外径)
圧縮応力 σx と引張応力 σy の軸方向に振動する偏波(光)の実効屈折率変化 Δnx とΔny の間には、光弾性効果による関係式があり、文献[12]より、以下の式のように表される。
Δnx – Δny ≒ -4f C / (πb) (C:光弾性定数)より Δnx < Δny となる。
媒質中の光速度 v = c / n (c:真空中の光速度、n:媒質中の光速度)
上式より、非軸対称の外力を加えた x 軸方向の実効屈折率変化 Δnx が、y 軸の実効屈折率変化 Δny より低いため、x 軸方向の光速度 vx が速波モードになる。
従って、速波モードと遅波モードの間の相対位相差 Δϕ は、以下の式で表される[12]、[13]。
Δϕ = (8C/λb) ΔfL = (8C/λb) ΔW
図26の⑧の実験結果より、相対位相差 Δϕ と相対荷重 ΔW の関係は、リニアであることが分かったため、その傾き角度が、(8C/λb) に相当し、λ と b は既知の値なので、上式より光弾性定数 C が求められる[12]、[13]。
図27の②は、偏波面保存ファイバ(PMF)の代表的なPANDAファイバの断面写真である。パンダの目に相当する黒丸部分は、応力付与部と言われ、熱膨張係数(熱収縮率)が大きいボロン(B2O4)という材料が添加されている。光ファイバの大部分の白くなっているクラッド部分の材料は石英ガラス(SiO2)である。光ファイバを製造する際、約1500℃のヒートゾーンを持つ高温炉へ挿入して焼結・透明ガラス化するが、室温まで急激に冷却する間にパンダの黒目の部分の応力付与部のボロンと石英ガラスの熱収縮率の違いにより非軸対称の主応力成分が発生する。黒目の部分は縮もうとして円の内径が小さくなるよう引張応力が強くなるので、光ファイバの中心のコア部分の y 軸方向(パンダの目)に引張応力が発生し、x 軸方向(パンダの頭)にはその反対の圧縮応力が発生する。従って、図27の①の場合と同じように、x 軸方向から非軸対称外部応力が加わった場合と同じになり、パンダの頭方向には圧縮応力が発生し、それに直交する黒目の方向には、引張応力が発生するため、頭の部分の屈折率が低くなるため速波軸(Fast Axis)になり、黒目の部分は引張応力になるので屈折率が高くなり遅波軸(Slow Axis)となる。
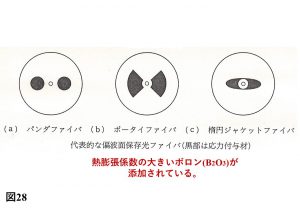
図28に、内部応力付与型の代表的な3つの偏波面保存ファイバ(PMF)の断面図を示す。
(a)パンダ(PANDA)ファイバ[14]、(b)ボータイ(Bow-tie)ファイバ[15]、(c)楕円ジャケットファイバ[16],[17]
これらの内部応力付与型の偏波面保存ファイバの構造の最大の特徴は、筆者の論文で提案している一方向外力に起因する非軸対称の応力差により発生する光弾性効果を利用していることである[12],[13]。クラッド材料(石英ガラス:SiO2)に比べて熱収縮率が非常に大きい黒い部分の応力付与材料(SAP:Stress Applying Parts)のボロン(B2O4)を、コアを挟むように入れ、光弾性効果を使って複屈折率性を持たせる応力付与型と、コアの縦横で実効屈折率を変化させた幾何学的非軸対称型[18]がある。一般的には、応力付与型が多く使われており、主に応力付与材をパンダの目のように丸型にしたNTT研究所や日本の光ファイバメーカ(フジクラ、住友電工、古河電工)で研究開発されたPANDA型や、英国のサウサンプトン大学(University of Southampton)で研究開発された蝶ネクタイ型にしたボウタイ(Bow-tie)型[15]が広く使用されている。日立製作所中央研究所[16]、KDD研究所[17]や日立電線で研究開発された楕円クラッド型でコアの周りにシリカ(石英ガラス:SiO2)の低屈折率層を有する楕円ジャケットファイバは、前者に比べマーケットのシェアは狭いようである。
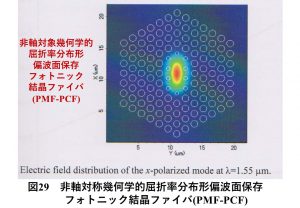
図29に、琉大大学院波平研究室で研究していた、新しいフォトニック結晶ファイバ(PCF:Photonic Crystal Fiber)の非軸対称幾何学的屈折率分布形偏波面保存フォトニック結晶ファイバ(PMF-PCF)の構造例を示す。
図29は、筆者のPh.D.の教え子のバングラデシュ出身の留学生で、現在バングラデシュで別々の大学で教授として活躍しているProf. Dr. S.M. Abdur Razzak[19]と Prof. Dr. Md. Anwar Hossain[20]と筆者との連名の研究論文に用いた偏波面保存形フォトニック結晶ファイバの数値モデルの一例である。フォトニック結晶ファイバは、コアは石英ガラスで、クラッド部分を周期的な空孔を配列して光伝送をする新しいタイプの光ファイバであるが、空孔の配列を幾何学的に図29のように非軸対称にすることで偏波面保存性を高くすることができることを実証している[19],[20]。
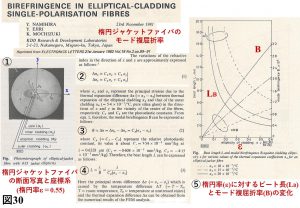
図30に、筆者が楕円ジャケット型偏波面保存ファイバのモード複屈折率を有限要素法(FEM:Finite Element Method)を使用して、応力の数値解析を行い、楕円ジャケットの応力付与部の楕円率 ε に起因して発生する内部応力と光弾性効果による実効屈折率変化 Δn よりビート長 LB とモード複屈折率 B の関係を明らかにすることができた[17]。楕円ジャケット型偏波面保存ファイバは、KDD(KDDI)研究所と日立製作中央研究所との共同研究の成果の一部で、光ファイバは日立製作中央研究所で製作されたものである。
図30で、①、②、③及び④の概要を以下に示す。
① 楕円ジャケットファイバの断面写真と座標系(楕円率 ε = 0.55)(日立製作中央研究所製[16])
② 光弾性効果による実効屈折率変化 Δn
③ 光弾性効果によるモード複屈折率 B
④ 光弾性効果によるビート長 LB
図30より、楕円率 ε が大きくなると、内部応力が大きくなり、光弾性効果により、実効屈折率変化 Δn が大きくなるのでモード複屈折率 B も大きくなり、ビート長 LB は短くなることが分かる。このビート長 LB より、偏波モード分散(PMD:Porarization Mode Dispersion)が求められる。
前述したように、楕円ジャケット型偏波面保存ファイバは、KDD研究所の筆者と日立製作中央研究所の松村宏善氏(理学博士)との共同研究の成果の一部である。楕円ジャケット型偏波面保存ファイバを開発された日立製作中央研究所の松村宏善博士が英国のサウサンプトン大学で、光ファイバの開発等で世界的に著名なProf. Dr. W. A. Gambling先生のResearch Fellowとして研究されていた頃、筆者がサウサンプトン大学を訪問した時に初めて松村氏にお会いした頃からの古い友人である。サウサンプトン大学は、ロンドンから南方へ約1時間鉄道で行ったところにあり、1912年4月10日に、不沈と言われたタイタニック号が米国のニューヨークへ向け処女航海に出港したサウサンプトン港がある港町にある光ファイバ通信関連では世界的に有名な大学で、日本からの留学が多い大学でもある。
また、松村氏と同様にProf. Dr. W. A. Gambling先生のResearch FellowをしておられたProf. Dr. D. N. Payne先生(元オプトエレクトロニクス研究所長)は、ファイバレーザー、エルビウムドープファイバ(EDFA)やボータイファイバなどの発明者で世界的に著名な先生で筆者の古い友人でもある。
松村氏とProf. Dr. D. N. Payne先生は、ほぼ同年代で研究者としてのライバルではあるがお互い良き友人でもある。松村氏がサウサンプトン大学での研究を終えて、日本に帰国して最初に研究されたのがこの楕円ジャケット型偏波面保存ファイバの発明である。また、ほぼ同時期に、Prof. Dr. D. N. Payne先生も蝶ネクタイ型のボウタイ型偏波面保存ファイバを発明されており、これらが筆者の非軸対称外力に起因する偏波面保存ファイバの基本原理である論文の発表時期と2種類の偏波面保存ファイバの発明に関わっていたことは、非常に感慨深いものがある。
次は、PMDの基本原理と国際標準化について述べる予定である。
[参考文献]
[12]波平宜敬、工藤正昭、虫明康人;“光ファイバの伝送特性に及ぼす機械的圧力の影響”、信学論、Vol.63, No.7, pp.391-398, 1977.
[13] Y. Namihira;“Opto-elastic constant in single mode optical fibers”, IEEE, Journal of Lightwave Technology, Vol.LT-5, pp.1078-1083, Oct., 1985.
[14] Y. Sasaki, et al.,”Polarization-maintaining and absorption-reducing fibers,”5th OFC’82, Phoenix, AZ, 1982.
[15] R. D. Birch et al.,”Fabrication of polarization maintaining fibers using gas-phase etching,”Electron.,Lett.,V.18, No.24, pp.1036-1038, 1982.
[16] H. Matsumura et.al.,”Fundamental study of single-polarization fibers,”6th European Conference on Optical Communication(ECOC), York(UK), pp.49-52, 1980.
[17] Y. Namihira, et al.,“Birefringence in elliptical-cladding single-polarisation fibre”, Electron. Lett., Vol.18, No.2, pp.89-91, Jan., 1982.
[18] T. Okoshi et al.,”Side-tunnel fiber:An approach to polarization-maintaining optical waveguiding scheme”, IEE, Electron.Lett.,Vol.18, No.19, 1982.
[19] S. M. A. Razzak, Y. Namihira, “Highly birefringent photonic crystal fibers with near-zero dispersion at 1550 nm wavelength,” Journal of Modern Optics (Taylor & Francis), vol. 56, no. 10, pp. 1188-1193, June 2009.
[20] M. A. Hossain, Y. Namihira et al., “Polarization maintaining highly nonlinear photonic crystal fiber for supercontinuum generation at 1.55 μm,” Optics & Laser Technology, vol. 44, no.5, pp.1261-1269, July 2012.
次回へ続く